Validating UTF8 strings with Lookup Tables

Validating UTF8 strings with Lookup Tables

A recent post appearing on Daniel Lemire's blog heralds a new performance milestone in SIMD utf8 string validity verification using AVX(256 bits) instructions.  While AVX performance on some existing hardware might actually be pessimization*, the older 128 bit  SIMD version should still be blazingly fast on most systems.

Checking for utf8 string validity using SIMD intrinsics is the logical performance optimization to make (having significant experience with this myself). However, in reaching first for our largest optimization hammer, have we  have we prematurely neglected the possible performant scalar solutions? In particular the state machine like nature of utf8 string validity checking strongly suggests a lookup table type of solution.

So how might a non SIMD,  lookup table (effectively 16 bit) version operate? And what might be its performance? Lookup table based utf8 validate can out perform SIMD-128bit utf8 validate but does not do so on average due to caching effects.

Lookup Table Naive Implementation

First like other utf-8 validating schemes we start with a decoder state. However, due to the fact that we will be using these in lookup tables we will try to reduce the total number of states to as small as possible (with utf8 decode rules appearing in Lemire's post). Below appears the table that maps the next state for each consumed byte (hex) to a enum.

Complete non-degenerate decoder state graph

Once we have our states we can begin with our initial naive lookup table implementation.  Our initial implementation will be a single table that takes in the current state and the current charbyte of the array and maps it to the next decoder state. This table is is simple to construct taking a brute force 2^(4+8) operations. Below is a graphical illustration of execution with the propagation of the decoding state.

Flow of decoder state passing through lookup tables

In code it is simply:

uint8_t runState = READY_NEW;
while (len > 0)
{
runState = tableDecode[ *src++  | (runState<< 8)];
len--;
}


So how does this naive implementation perform? The answer is not that well at all! It beats a branching and testing implementation but isnt anywhere close to the original SIMD-128 version published by Lemaire.

The problem with this naive lookup table approach is the latency of a memory load.  Even for data in L1 cache the latency of a indexed lookup is at least 5 cycles. The fastest this naive approach will ever be is 5 cycles per byte. While modern hardware can issue multiple instructions in a single cycle (otherwise known as superscalar) the data dependency here prevents this technique from providing any additional performance.  To go beyond this naive implementation we need to reduce instruction dependencies and decode more than one byte at a time.

Naive Lookup Implementation will take at least 5 cycles per byte

Chained Superposition Implementation

In order to reduce instruction dependence we are going to have to produce and chain lookups with values that are in superposition to all possible decode states that could have come before. The initial decode translation will also operate on two bytes at a time via a 16 bit lookup table.


While it might sound insanely complex it turns out that there are only a small number of superpositions for all possible chaining of superposition lookups. (20 possible superpositions for any 2 byte lookup and a total of 52 superpositions for all possible chains)

Given the small number of superpositions these can be represented as simple numbers of 6 bits and can be chained using a 6 + 6 = 12  bit lookup table. Below is a cycle graph as to how this new version might be executed in time.

In full details the code of the validation loop looks something like this:

const uint16_t* asShort = reinterpret_cast<const uint16_t*>(src);
const uint16_t* asShortEnd = &asShort[len / sizeof(uint16_t)];
uint8_t runCon = runState;
while (asShort != asShortEnd)
{
uint8_t decoded0 = tableDecode[*asShort++];
uint8_t decoded1 = tableDecode[*asShort++];
uint8_t decoded2 = tableDecode[*asShort++];
uint8_t decoded3 = tableDecode[*asShort++];
uint8_t prejoin0 = tableJoin[(decoded0 << 6) | decoded1 ];
uint8_t prejoin1 = tableJoin[(decoded2 << 6) | decoded3 ];
uint8_t toCon = tableJoin[(prejoin0 << 6)| prejoin1];
runCon = tableConcate[ runCon | (toCon << 4)];
}

Results and Comparisons

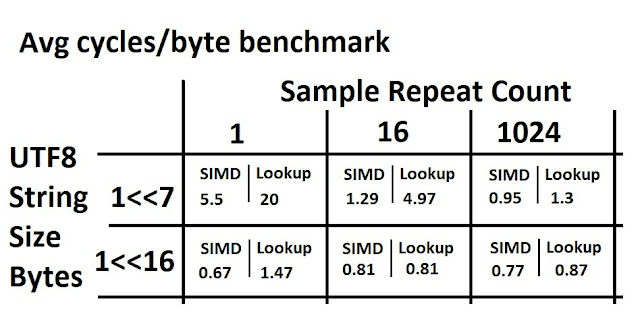
Since Lemire provided full source and benchmark for his original SIMD version we are able to do a direct performance comparison between the SIMD-128bit version and the chained superposition lookup table algorithm. Below are tables reporting this comparison for both minimum number cycles/byte performance and average number of cycles/byte performance. Note that sample repeats were made on a unique random utf8 string for every repeat (this is important as timing the same string repeatedly would favor a lookup table solution).

The results actually correspond to general expectations. The lookup table driven algorithm requires a hot cache to perform anywhere close to the SIMD-128 version thus the performance is only comparable for large strings or high sample repeats.  As it stands the performance can be summarized as follows: In the limit of long strings and repeated usage Lookup Table is still 6% minimum slower and %12 slower on average than SIMD-128bit.

Discussion and Conclusion

While still slightly slower on average it is quite remarkable that an algorithm that works in effectively 16 bits can be competitive with a 128 bit SIMD algorithm. Even more surprising is that it can, under certain conditions, exceed the speed of code that makes use of these powerful "vector" instructions.

Here are the suggested reasons why the table based approach achieves such performance:

1.  Superscalar machines perform SIMD-like operations automatically by issuing multiple instructions per cycle.
2. Lookup tables perform computations in a manner such that they are in effect creating new instructions custom fit for the algorithms specific purpose.
3. Caching behavior causes lookup table algorithms to increase in performance for specific data Values (working similar the effects of branch prediction ). 

So what conclusions can we draw from this exercise? Should we validate utf8 strings with lookup tables? Not likely. The lookup tables require creation and causes cache pollution.  However one might pause and wonder if this type of performance can be obtained from a machine that isn't designed for these type of operations what might the performance might be attained on hardware with a different design?

Ref

*AVX performance issues
Despite having a less than 2 year old cpu (i7-6700HQ) with AVX2 support the newer AVX version published by Lemire is actually always significantly slower (~30%) than his original SIMD-128bit version on my machine. What is the nature of this unexpected pessimization is not clear.


My full table lookup utf8 validity checking algorithm can be found here:
https://github.com/darkcephas/utf8Validity_lookupTable


ScreenToGif was used to create animations

Update:
Very similar implementation https://bjoern.hoehrmann.de/utf-8/decoder/dfa/